Interest Rate-利率

A small amount of money now may be equivalent in value to a larger amount received at a future date.
一小笔现在的前，可能相当于未来某一时间的更大金额.

Interest rates are set in the marketplace by the forces of supply and demand.
利率在市场上由供求决定

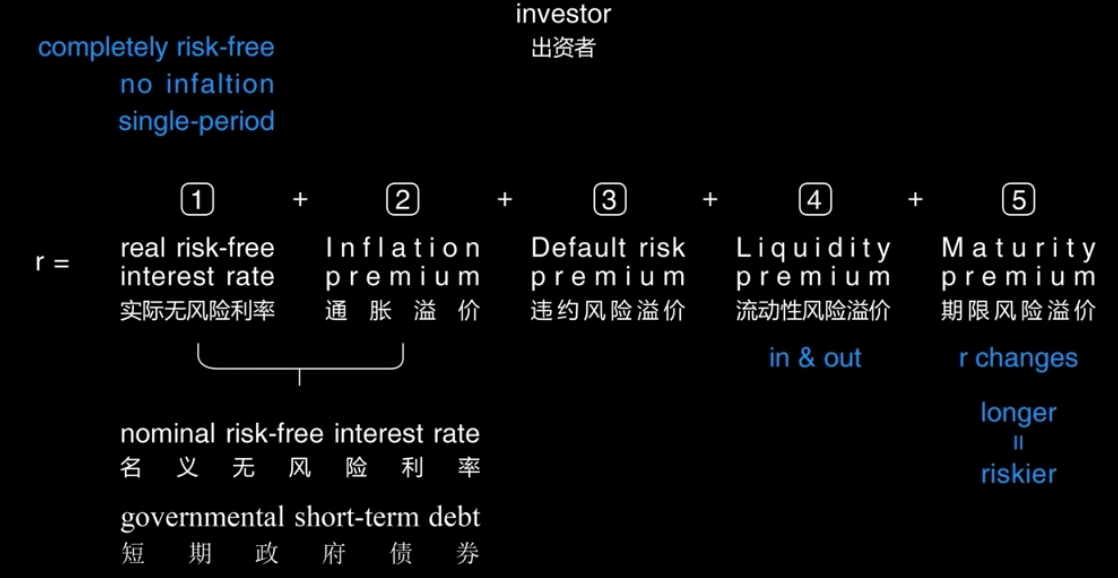※一些短期政府债券也被视为名义无风险利率

利率也被称为

required rate of return-必要回报率
discount rate-折现率
opportunity cost-机会成本

opportunity cost is the value that investors forgo by choosing a particular course of action
机会成本是投资者选择了某个行为而放弃掉的价值

The time value of money-货币的时间价值

The time value of money as a topic in investment deals with equivalence relationships between cash flows with different rate
作为投资领域的一个概念，货币的时间价值处理的是不同日期之间的现金流的等价关系

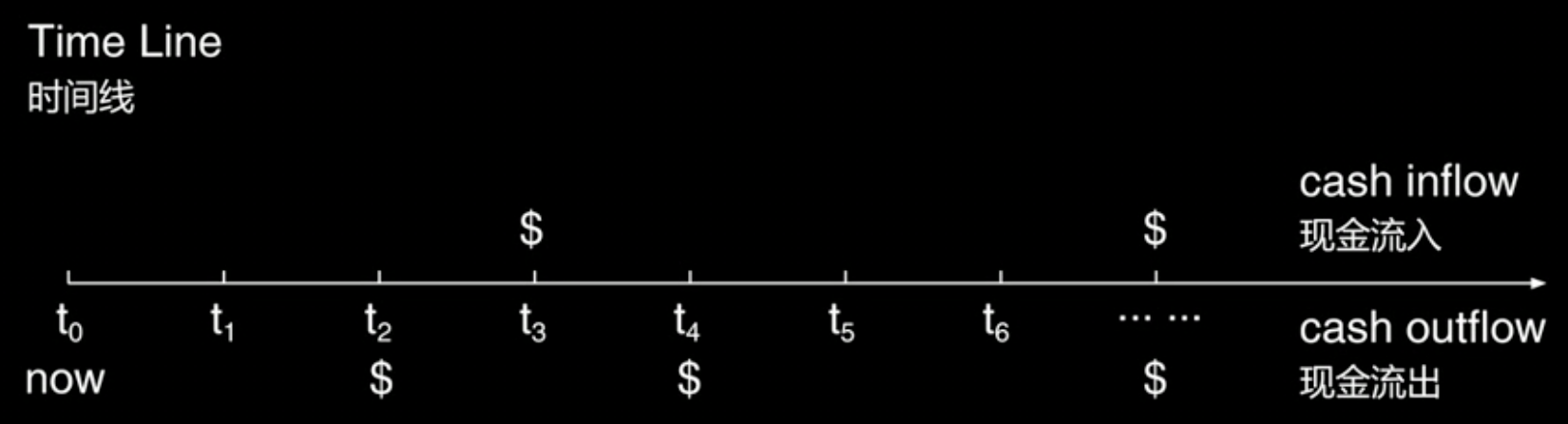※时间线上方出现的数字代表现金流入，下方出现的数字代表现金流出(不论带不带符号)

The Future Value of a Single Cash Flow-单一现金流的未来价值

Principle is the amount of funds originally invested
本金是最初的投资金额

The Frequency of Compounding-复利的频率

Continuous Compounding-连续复利

统计学中，数据分为
- continuous data 连续数据 (在一定区间内可以任意取值的数据叫连续数据。比如：体重：0.542..kg, 时间:1.234...s)
- discrete data 离散数据 (离散数据是指其数值只能用自然数或整数单位计算的数据。比如: 硬币:1个 学生:5个)

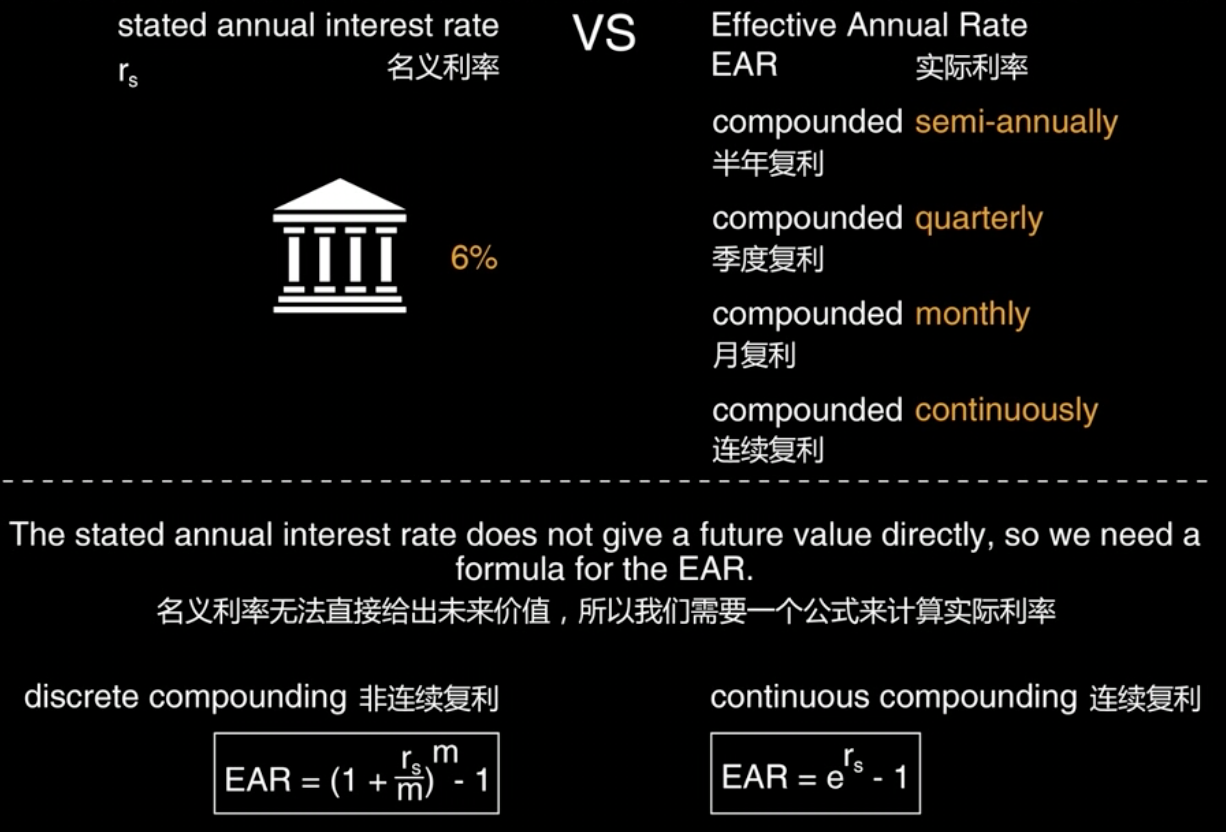
Stated and Effective Rates-名义利率和实际利率

假设名义利率为6%，计息期数为1年，根据计息频率

Frequency	rate of interest per period	number of period	FV
annually 每年	6% / 1 = 6%	1 * 1 = 1	1.06	1.06
semi-annually 每半年	6% / 2 = 3%	2 * 1 = 2	1.03 ** 2	1.0609
quarterly 每季度	6% / 4 = 1.5%	4 * 1 = 4	1.015 ** 4	1.061364
monthly 每月	6% / 12 = 0.5%	12 * 1 = 12	1.005 ** 12	1.061678
daily 每日	6% / 365 = 0.0164%	365 * 1 = 365	1.00164 ** 365	1.061831
continuously 连续	6%	1	e ** (0.06 * 1)	1.061837

FV中的**2代表平方

This result leads us to a distinction between the stated annual interest rate and the effective annual rate(EAR)
这个结果引出我们要讨论的名义年利率和实际年利率的区别

Python代码实现

import numpy as np

class Quantitative:
    def EAR_get(self,rs,m=None) -> float:
        """
        获取实际利率(Effectice Annual Rate)
        In:
        rs: 名义利率
        m:  计息频次, None代表连续计息
        Out:
        EAR：实际利率
        """
        if not m:
            ear = np.exp(rs) - 1
        else:
            ear = (1 + rs/m) ** m - 1
        return rar

    def fv_get(self,pv,rs,N,m=None) ->float:
        """
        获取单一现金流的未来价值
        In:
        pv:现在价值
        rs:名义利率
        N：计息期数
        m:计息频次,None代表连续计息
        Out:
        fv:未来价值
        """
        ear = self.EAR_get(rs,m)
        fv = pv * ((1+ear) ** N)
        return fv